|
Fathom:
- Open Fathom on your computer
- Click and drag a new graph into the screen
- Click on the "Empty Plot" box in the upper right hand
corner of the graph and change this to "Function Plot"
- Insert a slider from the "Insert" menu.
- Change the slider title from "V1" to "a"
- Double click on the slider and change its range so
that -5<a<5
- Repeat steps 4-6 to insert two additional sliders,
naming them "h" and "k" respectively.
- Right click on your graph and select "Plot Function"
- In the function expression box, type a(x-h)^2+k
and click ok
- What parent function does this look like?
- Move the slider for a. How does this affect the
graph? What happens when a is negative?
- Move the slider for h. How does this affect the
graph? What happens when h is negative?
- Move the slider for k. How does this affect the
graph? What happens when k is negative?
- Write a rule for how to perform each type of
transformation on a parent function by changing its equation.
- Describe in words how y=(x-2)^2 + 3 will transform
the parent function y=x^2. Move your sliders for a, h, and k to check your answer.
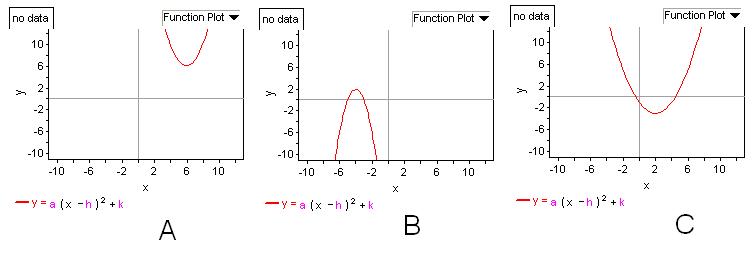
- Move the sliders to make your graph match graphs 1,
2, and 3. What are your values for a, h, and k for each of these graphs? Write a formula for each graph by
substituting a, h, and k into your function formula.
- Do the rules that you wrote for function transformation
work for all types of functions? Experiment with absolute value functions or cubic functions to find out.
- Double click on the formula of your graph and change
it to a|x-h|+k. Move the sliders around to see if they transform the graph in the same way as the graph of x^2.
- Repeat this process with the formula a(x-h)^3+k.
Graphing Calculators
- Set your graphing calculator to the standard graphing
window (zoom 6)
- On the same screen, graph: y=x^2, y=x^2+2, and y=x^2-2
- What do you notice about the graphs?
- How does the k in y=a(x-h)^2+k transform the graph?
- On a new screen, graph: y=x^2, y=(x-3)^2, and
y=(x+3)^2
- What do you notice about the graphs?
- How does the h in y=a(x-h)^2+k transform the graph?
- On a new screen, graph: y=x^2, y=2x^2, and y=(1/2)x^2
- What do you notice about the graphs?
- How does the a in y=a(x-h)^2+k transform the graph?
What happens if 0<a<1? a>1?
- Graph y=2x^2 and y=-2x^2 on a new screen. What
happens when a is negative? What type of transformation is this?
- Write a rule for how to perform each type of transformation
on a parent function by changing its equation.
- Describe in words how y=(x-2)^2 + 3 will transform
the parent function y=x^2. Graph this function on your graphing calculator along with y=x^2 to check your answer.
- Use what you have learned to write a formula for the
graphs of A, B, and C above.
- Do the rules that you wrote for function transformation apply to all types of
functions? Repeat steps 2-11 using the absolute value function |x| (or abs(x) in your calculator) and again using the
x^3 function. Do the same rules apply?
Use what you have learned to complete the homework.
|
 |